Difference Equations and

Recursive Relations

1751-1800


Number theory index History Topics Index

 A few of the relavant mathematicians that we shall lood at from this time period are: Euler, Johan Bernoulli III, G. Monge, and Laplace.
 
 




           click here for a full history and biography
 of Euler






The first mathematician that we shall look at is Euler.  He introduced beta and gamma functions, and integrating factors for differential equations.

In 1755 Euler published Institutiones calculi differentialis which begins with a study of the calculus of finite differences. The work makes a thorough investigation
of how differentiation behaves under substitutions.

In Institutiones calculi integralis (1768-70) Euler made a thorough investigation of integrals which can be expressed in terms of elementary functions. He also
studied beta and gamma functions, which he had introduced first in 1729.  They were given the names beta function and gamma function by Binet and Gauss respectively. As well as investigating double integrals, Euler considered ordinary and partial differential equations in this work.

Problems in mathematical physics had led Euler to a wide study of differential equations. He considered linear equations with constant coefficients, second order
differential equations with variable coefficients, power series solutions of differential equations, a method of variation of constants, integrating factors, a method of
approximating solutions, and many others. When considering vibrating membranes, Euler was led to the Bessel equation which he solved by introducing Bessel
functions.

1.  One of the major contribution of Euler was introduction of Gamma function.  The gamma function defined by an integral is as follows:

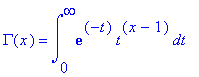
The gamma junction is a generalization of the factorial.  In fact, it has the following properties:

                                                             (1) 
                                                             (2) if n is a positive integer.
                                                             (3) 

A useful identity of the gamma fuction is

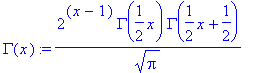
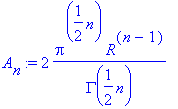
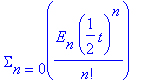
The formula for the surface area of the sphere {x2 + x2 +...x2 =R2 }  of radius R i n dimensions is

2.  The Euler numbers  En can be defined as:

or by the formula:

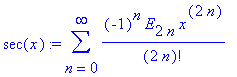
 All of the odd Euler numbers are 0.  The Euler numbers with odd subscripts vanish:  E2k+1 =0  for all k >0.  The non-zero Euler number are odd integers which alternate in sign.  The first few non-zero Euler numbers are:  E0 =1,  E2  =-1,  E4 =5,   E6 =-61,   E 8 =1385,   E10 =-50521,   E12 =2702765.
These Euler numbers, along with the Bernoulli numbers are helpful when attempting to approximate the Taylor series for complex functions involving the secant, tangent, and others that do not have simple formulas.
An example of the accompaning Bernoulli number is:

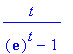which equals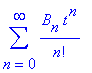 
For a more  discussion of Euler's numbers  visit mathworld.wolfram.com
  3.  Euler is also credited for the indroduction of the symbol for differences.   This simplified the representations of equations such as: 

or simply, .
 
 

The second mathematician we will look at is Johan Bernoulli III.  Click on his picture to see a  short biography.

In the field of mathematics he worked on probability, recurring decimals and the theory of equations.
 
 
 
 

The third mathematician we shall discuss is Laplace.

Click on Laplace's picture if you would like
to read his full biography.

One of Laplace's great works is the Traité du Mécanique Céleste published in 5 volumes, the first two in 1799.  The first volume of the Mécanique Céleste is divided into two books, the first on general laws of equilibrium and motion of solids and also fluids, while the secondbook is on the law of universal gravitation and the motions of the centres of gravity of the bodies in the solar system. The main mathematical approach here is the setting up of differential equations and solving them to describe the resulting motions. In this Laplace also developed the idea of the potential, which was appropriated from Lagrange (visit location),who had used it in his memoirs of 1773,  1777 and 1780.
  Laplace showed that the potential always satisfies the differential equation :

This equation is commonly expressed in a more general form, and  may be found in most branches of mathematical physics.  It is represented as follows:
A more descriptive explanation of Laplace and this equation may be found at this location.
Many numerical methods based on finite difference schemes have been used to solve this equation.
In 1794, Laplace and Lagrange used the method of variation of parameters to find a particular solution to linear inhomogeneous difference equations with variable coefficients.
  Between 1782-1812, Laplace proposes amethod of interpolation which includes "a preliminary introduction and development of the method of generating functions."
 
 
 
 

The last mathematician we shall mention is Gaspard Monge.
 
 

click on his picture for his biography.

Starting in 1771 and then over the next few years Monge submitted a series of important papers to the Académie on partial differential  and finite difference equations equations which he studied from a geometrical point of view.
 He is considered the father of differential geometry because of his work Application de l'analyse à la géométrie where he introduced the concept of lines of curvature of a surface in 3-space.