Difference Equations
and
Recursive Relations



 

Hindu-Arabic Period1

400 - 1200









The period from 400 - 1200 signified the dark ages in the history of mathematics. Little to no major accomplishments were made in Europe, those accomplishments that were made came mainly from the middle east. During this period we begin to see the emergence of difference equations, the following is a history of those equations and the mathematicians that influenced them.

The earliest major Indian mathematician was known as Brahmagupta. This mathematician introduced rules for solving simple quadratic equations of various types. He also invented a method for solving indeterminate equations of the second degree like the following:

a x2+1=y2

Brahmagupta was also the first person to publish a sinus table for any angle.

Brahmagupta's matrix is given as:

Powers of Brahmagupta's matrix are given as:
The  xn  and  yn  are called Brahmagupta's polynomials and are given by recursive relation:
xn+1  = x xn  + t y yn
yn+1  = x yn  + y xn
More information can be found in MathWorld.

Mathematicians, like Al-Karaji, furthered the work on the algebra of polynomials to include those of infinite terms. Al-Karaji also was the first to construct Pascal's triangle, and although this relationship was discovered independently by both the Persians and the Chinese in the eleventh century, including a well-known written description by Omar Khayyam, it is commonly mistakenly credited to its later European namesake.
 

Pascal's  triangle

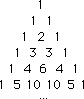
Another achievement in the algebra text is Khayyam's realisation that a cubic equation can have more than one solution. He demonstrated the existence of equations having two solutions, but unfortunately he does not appear to have found that a cubic can have three solutions. He did hope that "arithmetic solutions" might be found one day when he wrote :
                      Perhaps someone else who comes after us may find it out in the case, when there are not only the first three classes of known

                                                                       powers, namely the number, the thing and the square.

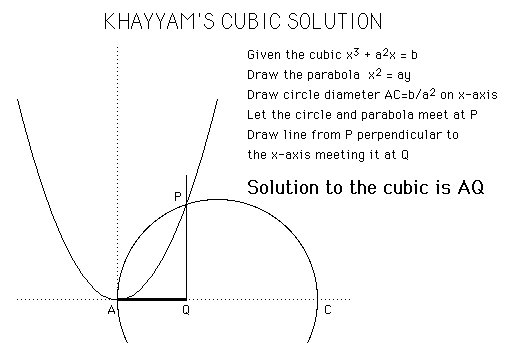
Khayyam's constuction for solving a cubic equation




Pascal's triangle is a triangular shaped arrangement of binomial coefficients in which the first row (n=0) is 1, the second row (n=1) is 1 1, the third row (n=2) is 1 2 1, and to on until the (n + 1)th row, kth column is defined by (N!)/((K!) (N-K)!)

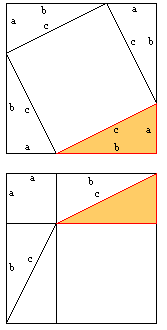
Further in this period the mathematician Bhaskara provided a proof of the Pythagorean theorem. His proof consisted of taking a square with a side of length C and dividing it into four equal triangles with sides of length A, B, and C, and a square with sides of length B-C (see below). He then set up the following relation of areas of the square:

(a+b) 2 = 4(.5ab) +   c2 = a2 + b2 + 2ab
it follows that c2 = a2 + b2

Bhaskara-Brouckner algorithm :

A sequence of approximations  to  can be derived by factoring 

(where -1 is possible only if -1 is a quadratic residue of n). Then 
 
and

Therefore, a and b are given by the recurrence relations

with . The error obtained using this method is 

The first few approximants to  are therefore given by 
 For the case n = 2, this gives the convergents to  as 1, 3/2, 7/5, 17/12, 41/29, 99/70, ... 
and the denominators are the Pell numbers.
 
 
 

The mathematician Al-Samawal writes al-Bahir fi'l-jabr (The brilliant in algebra). He develops algebra with polynomials using negative powers and zero. He solves quadratic equations, sums the squares of the first n natural numbers, and looks at combinatorial problems.
Al-Samawal furthered the work on Polynomial equations by being able to find the roots of a polynomial as well as solutions to quadratic equations. More importantly, he gave a full description of the binomial theorem with the coefficients given by Pascal's triangle.
Perhaps one of the most remarkable achievements in Book 2 of al-Bahir  is al-Samawal's use of an early form of induction. What he does is to demonstrate an argument for n = 1, then prove the case n = 2 based on his result for n = 1, then prove the case n = 3 based on his result for n = 2, and carry on to around n = 5 before remarking that one can continue the process indefinitely. Although this is not induction proper, it is a major step towards understanding inductive proofs. We should also comment that he was not the first to use this form of recursive reasoning, since al-Karaji had used similar methods. The result which al-Samawal himself was most proud is
 

                                                                                         12 + 22 + 32 + ... + n2 = n(n+1)(2n+1)/6
which does not appear in earlier texts.
 
 
 

The mathematician Al-Tusi also wrote on binomial coefficients, he was the first to find the roots of the cubic equation. In order to do this he first took the equation
 
 

X3 + A = BX

where A and B are positive and noted that if t is a solution then

t 3 + A = Bt

since A > 0, t 3 < Bt so t < B.5

next he notes that BX - X3 = A

and he finds the maximum of Y = BX - X3 occurs at X = (B / 3).5 which makes

max (Y) = 2 (B/3)3/2









He then deduces that the equation has a positive root

D = (B3 / 27) + (A3 / 4) > 0.






where D is the discriminant. Later he expanded this solution to what is now known the Ruffini-Horner approximation method.