Difference Equations

and

Recursive Relations

1826-1850

Main Page

Next topic

History Topics Index

Difference Equations and Recursive Relations have been studied intensively in this period.

Cauchy
One of Cauchy's contribution to differential equations is given by Cauchy's Functional equation.

f ( x + y ) = f (x) + f (y)

The most general continuous solution is:

f ( x ) = ax, where a is the constant.

The name is also given to the equation

f ( x + y ) = f ( x ) f ( y ),

known as the Cauchy-Abel equation, and to the pair of equations

f ( xy ) = f ( x ) + f ( y ),
f ( xy ) = f ( x ) f ( y ),

whose most solutions are given respectively by the equations:

f ( x ) = c log | x | , f ( x ) = 0,
f ( x ) = x, f ( x ) = 0.

Visit MathWorld

Airy
The general form of a homogeneous second order linear differential equation looks as follows:

y'' + p(t) y'+q(t) y=0.

The series solutions method is used primarily, when the coefficients p(t) or q(t) are non-constant.
One of the easiest examples of such a case is Airy's Equation

y''-t y = 0,

which is used in physics to model the defraction of light.
Thus the general form of the solutions to Airy's Equation is given by

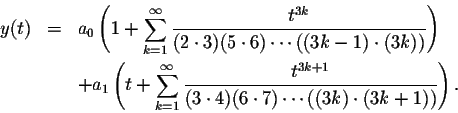
$\begin{eqnarray*}y(t)&=&a_0\left(1+\sum_{k=1}^\infty \frac{t^{3k}}{(2\cdot 3)(5\......{t^{3k+1}}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\right).\end{eqnarray*}$ Note that, as always, y(0)=a₀ and y'(0)=a₁. Thus it is trivial to determine a₀ and a₁ when you want to solve an initial value problem.
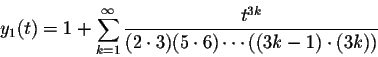
In particular $\begin{displaymath}y_1(t)= 1+\sum_{k=1}^\infty \frac{t^{3k}}{(2\cdot 3)(5\cdot 6)\cdots((3k-1)\cdot (3k))}\end{displaymath}$

and

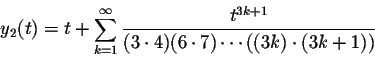
$\begin{displaymath}y_2(t)=t+\sum_{k=1}^\infty\frac{t^{3k+1}}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\end{displaymath}$

form a fundamental system of solutions for Airy's Differential Equation.

Sturm

Oscillation and transformation theory

of

symplectic difference systems

Symplectic difference systems are the first order recurrence systems

$\begin{displaymath}z_{k+1}= {\Cal S}_kz_k,\end{displaymath}$

(1)

where $z:\Bbb N\to \Bbb R^{2n}$ and ${\Cal S}:\Bbb N\to\Bbb R^{2n\times 2n}$ is a symplectic matrix, i. e. ${\Cal S}^T{\Cal J}{\Cal S}={\Cal J}$ with

$\begin{displaymath}{\Cal J}=\left(\begin{array}{cc}0 &I\\ -I &0\end{array}\right),\end{displaymath}$

I being the $n\times n$ identity matrix. Symplectic difference systems cover a large variety of difference equations and systems, among them as a very special case the second order Sturm-Liouville difference equation

$\begin{displaymath}\Delta (r_k\Delta x_k)=p_kx_{k+1}=0,\quad\Delta x_k:=x_{k+1}-x_k,\end{displaymath}$

(2)

whose oscillation theory is deeply developed.

Visit Sturmian sequence, Sturm Function

Verhulst
The basic mathematical model based in population studies is that the population size for one generation is proportional to the size of the previous generation. This is expressed mathematically by the following equation:

p_t+1 = r p_t (1)

where:

t	represents the time period (which could be minutes, weeks, years, etc. depending on the species being considered),
p_t	represents the population size at time t. The units of time could be hours, days, years, etc.,
p_t+1	represents the population size at the next time period. Again, it could be the next hour, next day, next year, etc., and
r	referred to as the Malthusian factor, is the multiple that determines the growth rate.

This growth equation can be used in cases where there is truly this type of growth. For example, when a new species arrives to an island where there is plentiful of food, perfect conditions for reproduction, and no predators, one can certainly observe this (almost perfect) type of growth; although, not forever. That is why other mathematical models were developed.
Limited growth. The problem with the equation (1) model is that the population continues to grow unlimited over time. A major contribution came from Pierre Francois Verhulst, a scientist interested in population growth. Verhulst was born in 1804 in Brussels, Belgium. He showed in 1846 that the population growth not only depends on the population size but also on how far this size is from its upper limit.

Let's look at the mathematics behind this.Carrying capacity is the maximum population size that a given habitat can support. We’ll denote that as K. If the population is far below K, it would tend to grow rapidly, but as it approaches K, the growth would slow down. If the population size would exceed its upper limit K, the growth would actually be negative!. In order to model this, Verhulst modified equation (1) to make the population size proportional to both the previous population and a new term:

(K- p_t )/K (2)

So the equation using this new term and named after Verhulst is:

p_t+1 = r p_t (K- p_t )/K (3)

This equation is also known as a logistic difference equation. Comparing it with equation (1) it is nonlinear in the sense that one can’t simply multiply the previous population by a factor. In this case the population p_t on the right of the equation is being multiplied by itself. One of the nice things about this equation is that it is relatively easy to solve and it is also easy to see how it behaves by looking at a chart produced by it. The following chart was produced with K = 1000, r = 1.3, and an initial value p₀ of 0.1:

The curve produced by the logistic equation resembles an S. That is why it is called an S-shaped curve or a Sigmoid. As you can see, when the population starts to grow, it does go through an exponential growth phase, but as it gets closer to the carrying capacity (approximately when the time step reaches 37), the growth slows down and it reaches a stable level. There are many examples in nature that show that when the environment is stable the maximum number of individuals in a population fluctuates near the carrying capacity of the environment. However, if the environment becomes unstable, the population size can have dramatic changes.
The logistic growth equation is a useful model for demonstrating the effects of density-dependent mechanisms in population growth. However, its utility in real populations is limited because the dynamics of populations are complex and because it is difficult to come up with the real value for K in a given habitat. In addition, K is not a fixed number over time; it is always changing depending on many conditions.

Jacobi
In [9] Tom H. Koornwinder introduced the polynomials P_n^a,b,M,N(x) which are orthogonal on the interval [-1,1] with respect to the weight function

G(a+b+2)

2^a+b+1G(a+1) G(b+1)

(1-x)^a(1+x)^b +Md(x+1)+Nd(x-1),

where a > -1, b > -1, M ³ 0 and N ³ 0. We call these polynomials the generalized Jacobi polynomials, but sometimes they are also referred to as the Jacobi-type polynomials. As a limit case he also found the generalized Laguerre (or Laguerre-type) polynomials L_n^a,M(x) which are orthogonal on the interval [0,¥) with respect to the weight function

G(a+1)

x^ae^-x +Md(x),

where a > -1 and M ³ 0. These generalized Jacobi polynomials and generalized Laguerre polynomials are related by the limit

L_n^a,M(x) =

lim
b®¥

P_n^a,b,0,M

æ
ç
è

1 -

ö
÷
ø

In [3] we proved that for M > 0 the generalized Laguerre polynomials satisfy a unique differential equation of the form

¥
å
i = 0

a_i(x)y⁽ⁱ⁾(x)+x y¢¢(x)+ (a+1-x)y¢(x)+ny(x) = 0,

where a_i(x), for i ³ 0 are continuous functions on the real line and a_i(x) for i ³ 1 are independent of the degree n. In [1] Herman Bavinck found a new method to obtain the main result of [3]. This inversion method was found in a similar way as was done in [2] in the case of generalizations of the Charlier polynomials. See also [5] for more details. In [7] we used this inversion method to find all differential equations of the form

¥
å
i = 0

a_i(x)y⁽ⁱ⁾(x)+N

¥
å
i = 0

b_i(x)y⁽ⁱ⁾(x)

+MN

¥
å
i = 0

c_i(x)y⁽ⁱ⁾(x)+xy¢¢(x)+(a+1-x)y¢(x)+ny(x) = 0,

where the coefficients a_i(x), b_i(x) and c_i(x) for i ³ 1 are independent of n and the coefficients a₀(x), b₀(x) and c₀(x) are independent of x, satisfied by the Sobolev-type Laguerre polynomials L_n^a,M,N(x) which are orthogonal with respect to the inner product

< f , g > =

G(a+1)

ó
õ

x^ae^-xf(x)g(x)dx+Mf(0)g(0) +Nf¢(0)g¢(0),

where a > -1, M ³ 0 and N ³ 0. These Sobolev-type Laguerre polynomials L_n^a,M,N(x) are generalizations of the generalized Laguerre polynomials L_n^a,M(x). In fact we have

L_n^a,M,0(x) = L_n^a,M(x).

In [6] we used the inversion formula found in [5] to find differential equations of the form

¥
å
i = 0

a_i(x)y⁽ⁱ⁾(x)+N

¥
å
i = 0

b_i(x)y⁽ⁱ⁾(x)+MN

¥
å
i = 0

c_i(x)y⁽ⁱ⁾(x)

+(1-x²)y¢¢(x) +[b-a -(a+b+2)x] y¢(x)+n(n+a +b+1)y(x) = 0,

(1)

where the coefficients a_i(x), b_i(x) and c_i(x) for i ³ 1 are independent of n and the coefficients a₀(x), b₀(x) and c₀(x) are independent of x, satisfied by the generalized Jacobi polynomials P_n^a,b,M,N(x). We gave explicit representations for the coefficients a_i(x), b_i(x) and c_i(x) for i ³ 0 and we showed that this differential equation is uniquely determined. For M²+N² > 0 the order of this differential equation is infinite, except for a Î {0,1,2,¼} or bÎ {0,1,2,¼}. Moreover, the order equals

ì
ï
í
ï
î

2b+4

if M > 0, N = 0 and bÎ {0,1,2,¼}

2a+4

if M = 0, N > 0 and aÎ {0,1,2,¼}

2a+2b+6

if M > 0, N > 0 and a,bÎ {0,1,2,¼}.

For a = b = 0, M > 0 and N > 0 the generalized Jacobi polynomials reduce to the Krall polynomials studied by Lance L. Littlejohn in [13]. These Krall polynomials are generalizations of the Legendre type polynomials (a = b = 0 and N = M > 0) found by H.L. Krall in [11] and [12]. See also [10]. In [13] it is shown that the Krall polynomials satisfy a sixth order differential equation of the form (1). For a > -1, b = 0, M > 0 and N = 0 or for a = 0, b > -1, M = 0 and N > 0 the generalized Jacobi polynomials reduce to the Jacobi type polynomials which satisfy a fourth order differential equation of the form (1) ; see also [10], [11] and [12].

We emphasize that the case b = a and N = M is special in the sense that we can also find differential equations of the form

¥
å
i = 0

d_i(x)y⁽ⁱ⁾(x) +(1-x²)y¢¢(x) -2(a+1)xy¢(x) +n(n+2a+1)y(x) = 0,

(2)

where the coefficients d_i(x) for i ³ 1 are independent of n and d₀(x) is independent of x, satisfied by the symmetric generalized ultraspherical polynomials P_n^a,a,M,M(x). The Legendre type polynomials for instance satisfy a fourth order differential equation of the form (2). See [10], [11] and [12]. In [8] we found all differential equations of the form (2) satisfied by the polynomials P_n^a,a,M,M(x) for a > -1 and M ³ 0. In [4] we applied the special case b = a of the Jacobi inversion formula to solve the systems of equations obtained in [8].

Dirichlet
Dirichlet made significant contributions to differential equations. He is well recognized by his work with series. The Dirichlet series F ( s ) is of the form

                                                                                                                          ¥
                                                      å a _n n^-s f
                                                                                                                             n = 1
where s may be real or complex. F ( s ), the sum of the series, is called the generating function of   a _n . The simplest type of Dirichlet series is the Riemann zeta function in which a _n =1, for all values of n.
Visit Dirichlet Divisor Problem , Sierpinski's Prime Sequence Theorem, Sharing Problem

Liouville
Aside from Liouville's numbers, he also made contributions with Sturm to the foundations of oscillation theory for difference equations. For further knowledge of his work, scroll to Sturm's contibutions. Another important area which Liouville is remembered for today is that of transcendental numbers. He constructed an infinite class of transcendental numbers using continued fractions. In particular he gave an example of a transcendental number, the number now named the Liouville number
0.1100010000000000000000010000..., where there is a 1 in place n! and 0 elsewhere.
We may study constants by means of other constants. Given a real number 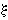, let R denote the set of all positive real numbers r for which the inequality

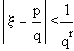
has at most finitely many solutions (p,q), where p and q>0 are integers. Define the Liouville-Roth constant (or irrationality measure)

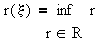
i.e., the critical rate threshold greater than which 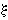is not approximable by rational numbers [1,2]. It's known that

x is rational	===>	r(x) = 1
x is algebraic irrational	===>	r(x) = 2
x is transcedental	===>	r(x) 2

If is a Liouville number, e.g.,

Catalan
The Catalan numbers (1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, ...), named after Eugène Charles Catalan
(1814--1894), arise in a number of problems in combinatorics. They can be computed using this formula:

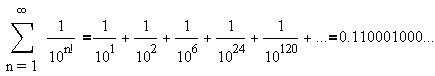
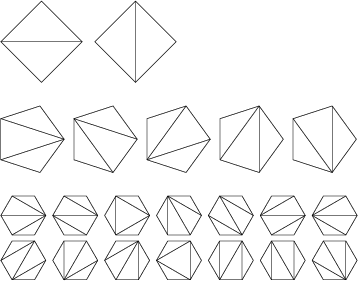
Among other things, the Catalan numbers describe the number of ways a polygon with n+2 sides can be cut into n triangles, the number of ways in which
parentheses can be placed in a sequence of numbers to be multiplied, two at a time; the number of rooted, trivalent trees with n+1 nodes; and the number of paths of
length 2n through an n-by-n grid that do not rise above the main diagonal.
An example is: 4 sides, 2 ways:

Super Catalan Number are given by the recurrence relation

with