Lyness' Equation

                Lyness' Equation has the form:
 

xn+1 = (a + xn )/ xn-1

where the parameter a > 0, x _n-1 > 0, x₀ > 0.

---

          The invariant of this equation is:
 

I(xn , xn-1 ) = (1+1/xn )(1+1/xn-1 )(a+xn +xn-1 )

    The Lyness equation has the equilibrium value:
 

p=(1±(1+ 4a)1/2)/2

 

THEOREM (Discrete version of  the Dirichlet's theorem).  Consider the difference equation

xn+1 = f( xn)

where x_n is in R^k and f: D® D is continuous, where D Ì R^k. Suppose that I:R^k® R is a continuous invariant that is I(f(x)) = I(x) for every x Î D. If I attains an isolated local minimum or maximum value at the equilibrium (fixed) point p of this system, then there exists a Liapunov function equal to ±(I(x) - I(p)) and so the equilibrium p is stable.
 

By using the above theorem, the Liapunov function, V(x,y) for this equation is found to be given by:
 

V(x, y)= I(x, y)-I(p, p)= I(x, y) - (p+1)3 /p V(x, y)=(1+1/x)(1+1/y)(a+x+y)-(p+1)3 /p

---

3-d  Plot of the Invariant of Lyness' Equation

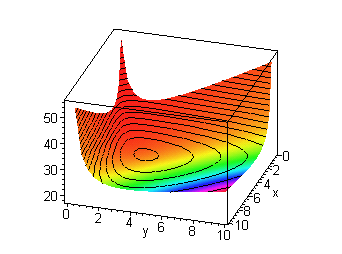
View an animated version of the above graph.

For more information about Lyness' Equation:

• Geometric Unfolding of a Difference Equation  a lecture by:

   Sir Christopher Zeeman
       "Technical skill is mastery of complexity while creativity is mastery of simplicity."
                            Catastrophe Theory, 1977.

Click here to go to Home Page for Difference Equations at URI
 

Click here to simulate the solutions of this equation for different choices of parameters and initial points